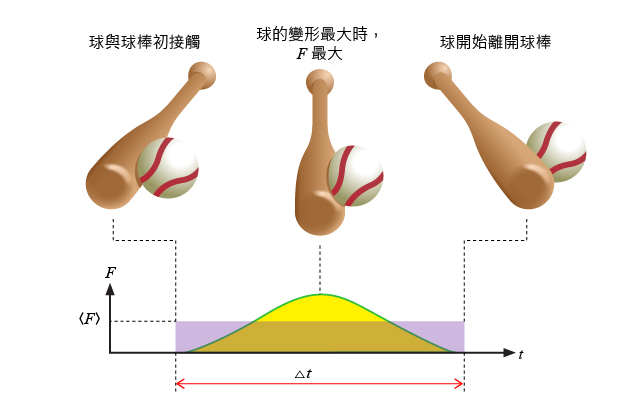
發生碰撞時,一股很大的力可能會在很短時間內作用在物體上。以棒球手擊球時的情況為例(),在球與球棒接觸的一剎那,力會作用於球上,改變球的速度。
再者,碰撞時,物體可能會短暫變形,過程中涉及能量的轉變:
那麼球對球棒的打擊力有多大呢?

設質量為 \(m\) 的球以速度 \(u\) 碰撞球棒,球反彈後的速度為 \(v\)。如果球受到球棒的作用力為 \(F\)、測得球碰撞球棒的時間是 \(\Delta t\),那麼,我們可以用曲線表示擊球過程中 \(F\) 與 \(t\) 的函數關係()。
通過分析 \(F\) 與 \(p\) 隨時間的變化,可知:
衝量 = 力 − 時間關係線圖下的面積
即是線圖下的黃色區域。
由於 \(F\) 隨時間而改變,它不容易被準確地直接量度出來。如果令 \(F\text{-}t\) 圖中矩形面積(紫色區域,即 \(\left\langle F \right\rangle \Delta t\))等於衝量,則 \(\left\langle F \right\rangle \) 稱為平均力。\(\left\langle F \right\rangle \) 的反作用力即球對球棒的平均打擊力。
總括而言,算式 \(F\Delta t=\Delta p\) 中的 \(F\),實際上是 \(\left\langle F \right\rangle \)。