如何計算載電導線在磁場中,所受到的磁力大小呢?
磁力亦為力的一種,所以用符號 \(F\) 來表示,單位是牛頓。
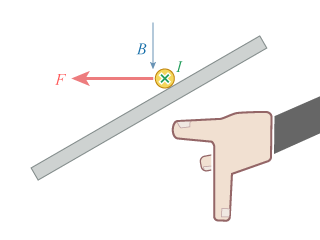
如所示,考慮在磁場 \(B\) 內有一根載有電流 \(I\) 的直導線。若電流方向與磁場之間的夾角是 \(\theta \),作用在導線上的磁力大小為:
\(F=B\ I\ l\ \sin \theta \)
其中 \(l\) 是導線在磁場中的長度。
留意在上式中:
【參考資料】當 \(\theta =90{}^\circ \),這相當於如之前的學習例子中,磁場與電流的方向均互相垂直。
當 \(B\) 與 \(I\) 並非互相垂直(但兩者不互相平行),便只有垂直於 \(I\) 的磁場分量會參與在導線作用磁力,即圖中的分量 \(B\ \sin \theta \)。若以弗林明左手定則判定磁力的方向時,食指便指向 \(B\ \sin \theta \) 的方向。
我們也可以用電流的分量來考慮,就是只有垂直於 \(B\) 的電流分量會受到磁力的作用,即 \(I\ \sin \theta \)。
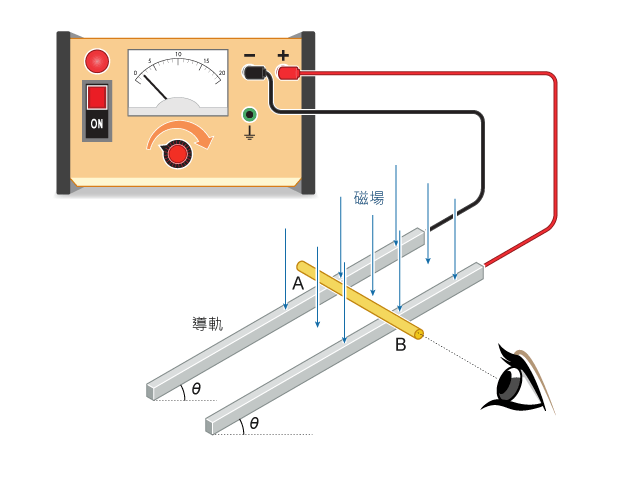
顯示在垂直指向下的勻強磁場中(場強等於 \(4 \text{ mT}\)),有一根置於光滑導軌上的金屬棒 \(AB\)。導軌如所示設有直流電源,提供 \(2 \text{ A}\) 的電流。若金屬棒長度等於 \(1.5 \text{ m}\)、導軌與水平之間的夾角為 \(30\) 度,試計算作用在金屬棒上的磁力。
【題解】
首先考慮作用在金屬棒上的磁力大小。
應用計算磁場施在載電導線上的磁力的算式:
\(F=B\ I\ l\ \sin \theta \)
\(=12\times {{10}^{-3}}\ \text{N}\)
再考慮作用在金屬棒上的磁力的方向。
應用弗林明左手定則,從棒的末端 \(B\) 觀察(見)可知:
作用於金屬棒的磁力的方向為 。
【參考資料】雖然導軌與水平之間的夾角為 \(30\) 度,但磁場與電流方向之間的夾角為直角,所以
\(\theta =90{}^\circ \)
由於電流的方向為從棒的末端 \(B\) 至末端 \(A\),換言之,根據弗林明左手定則,作用於金屬棒的磁力的方向便如圖中的箭咀 \(F\) 所示: