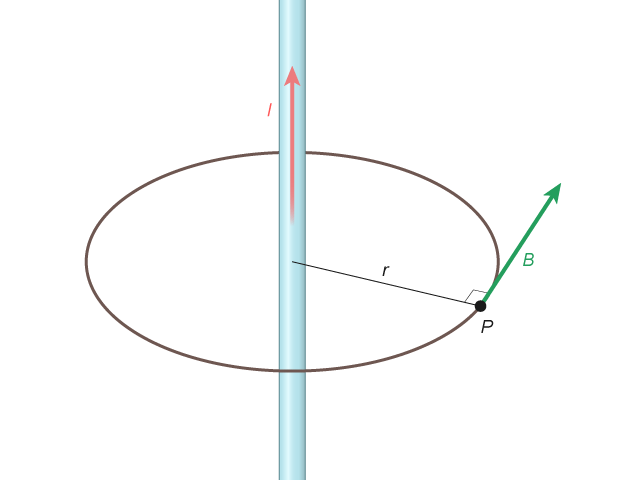
磁場的大小常以符號 \(B\) 來表示,單位是忒斯拉 (tesla),簡寫為 \(\text{T}\)。一根載電流 \(I\) 的長直導線,在導線外垂直距離為 \(r\) 的位置的磁場大小為(見):
\(\displaystyle{B=\frac{{{\mu }_{0}}I}{2\pi r}}\)
其中常數 \({{\mu }_{0}}=4\pi \times {{10}^{-7}}\ \text{T}\ \text{m}\ {{\text{A}}^{-1}}\),稱為真空磁導率。
上式乃假設了導線處於真空的環境。如果導線處於介質中,\({{\mu }_{0}}\) 需更改為該介質的磁導率 \(\mu \)。
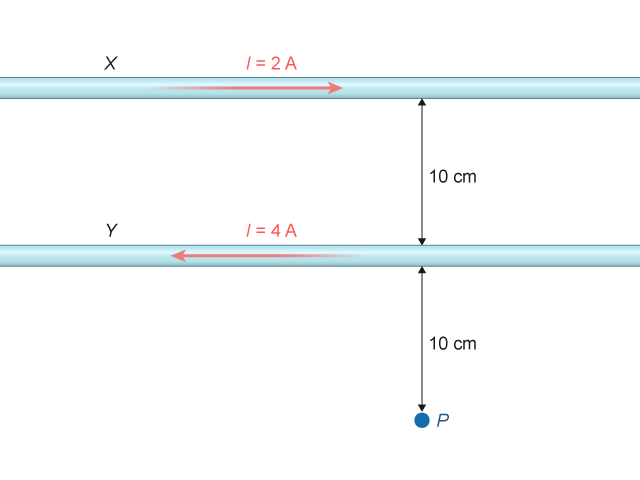
顯示兩條平行的長直導線之間相距 \(10 \text{ cm}\),導線 \(X\) 和 \(Y\) 分別載着 \(2 \text{ A}\) 和 \(4 \text{ A}\) 的電流,而且方向相反。試計算在兩條導線之外,距離 \(10 \text{ cm}\) 位置的點 \(P\) 的磁場。
【題解】
應用計算一條載電長直導線磁場的算式。
首先考慮源於導線 \(X\),在點 \(P\) 造成的磁場大小:
\(\displaystyle{{{B}_{X}}=4\pi \times {{10}^{-7}}\ \text{T}\ \text{m}\ {{\text{A}}^{-1}}\frac{2\ \text{A}}{2\pi \times 0.2\ \text{m}}}\)
\(=2\times {{10}^{-6}}\ \text{T}\)
再考慮源於導線 \(Y\),在點 \(P\) 造成的磁場大小:
\(\displaystyle{{{B}_{Y}}=4\pi \times {{10}^{-7}}\ \text{T}\ \text{m}\ {{\text{A}}^{-1}}\frac{4\ \text{A}}{2\pi \times 0.1\ \text{m}}}\)
\(=8\times {{10}^{-6}}\ \text{T}\)
由於磁場是向量,所以 \({{B}_{X}}\) 與 \({{B}_{Y}}\) 在點 \(P\) 的磁場合向量為:
【參考資料】根據長直導線的右手握拳定則,可知
換言之,
\(B={{B}_{Y}}-{{B}_{X}}\)
\(=6\times {{10}^{-6}}\ \text{T}\)
正數代表 \(B\) 的方向為指出紙面。