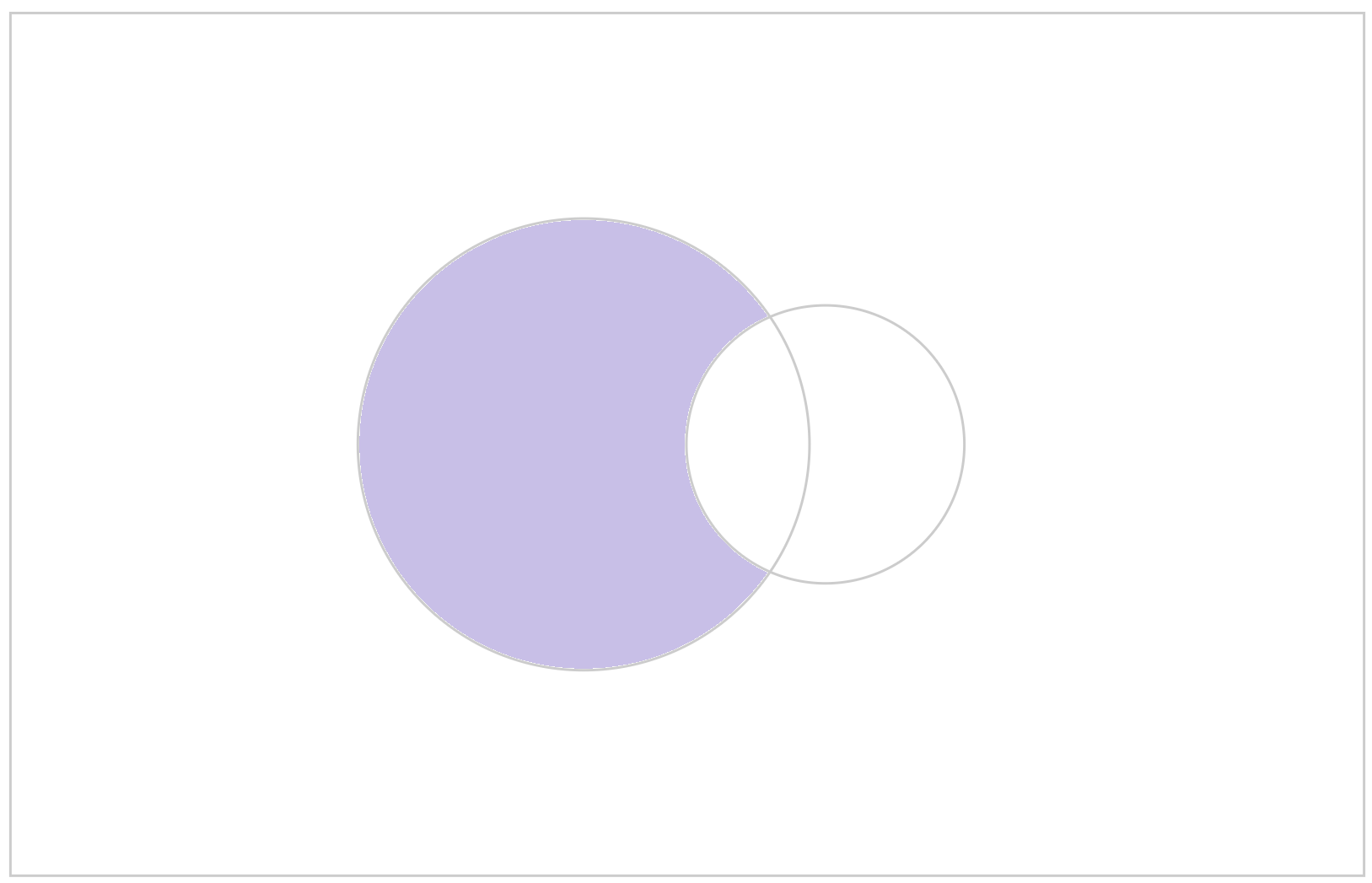
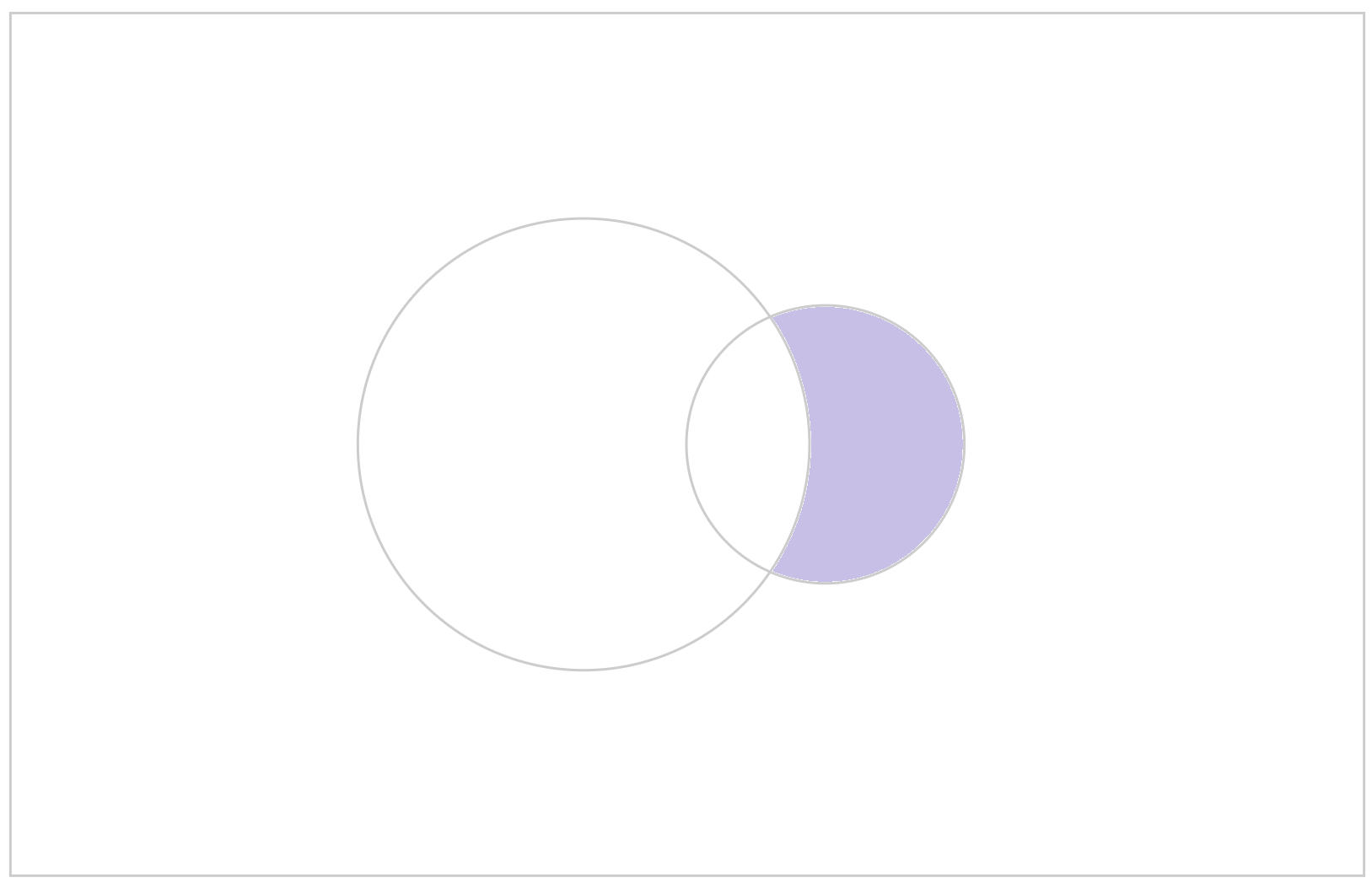
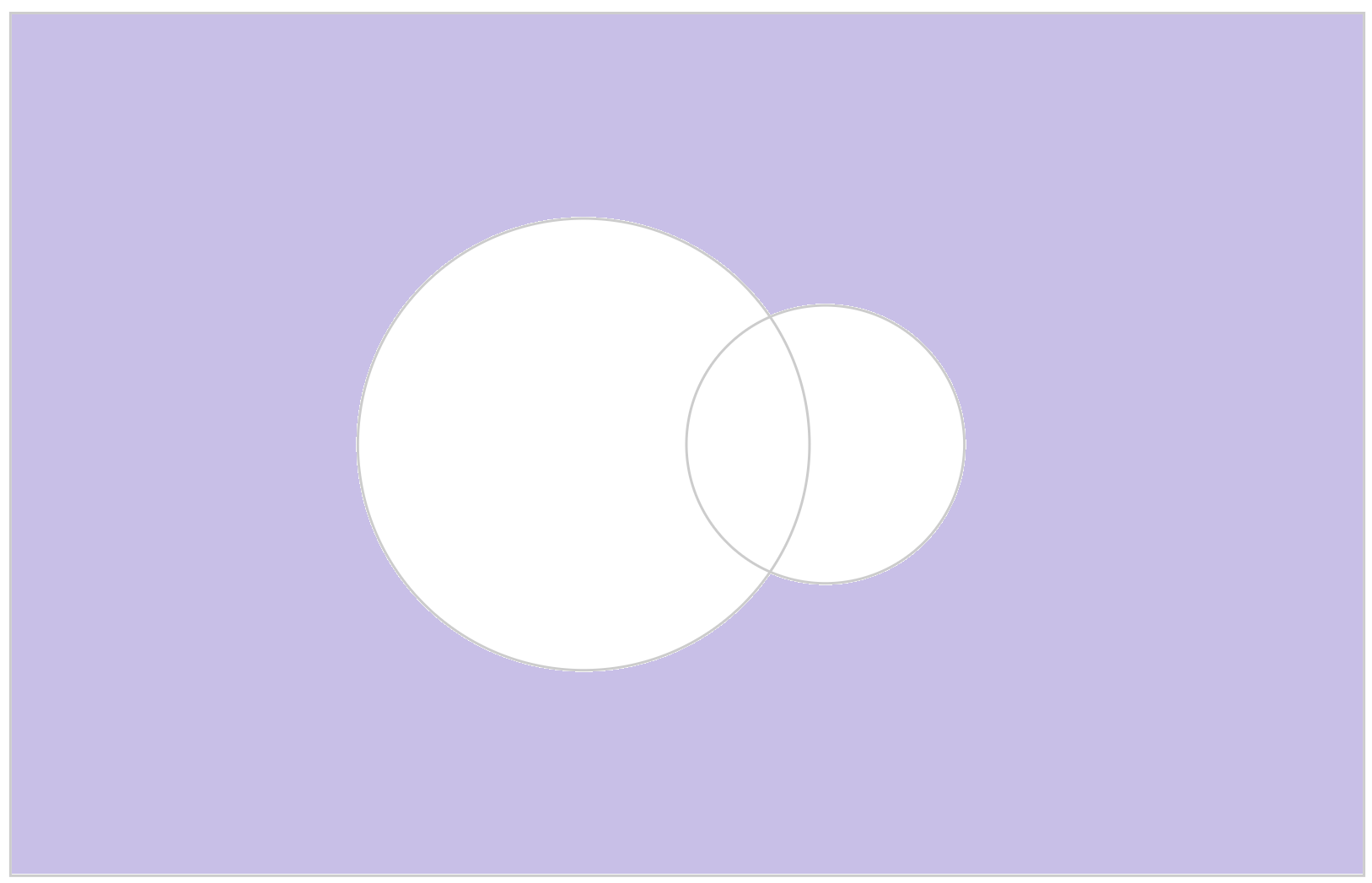
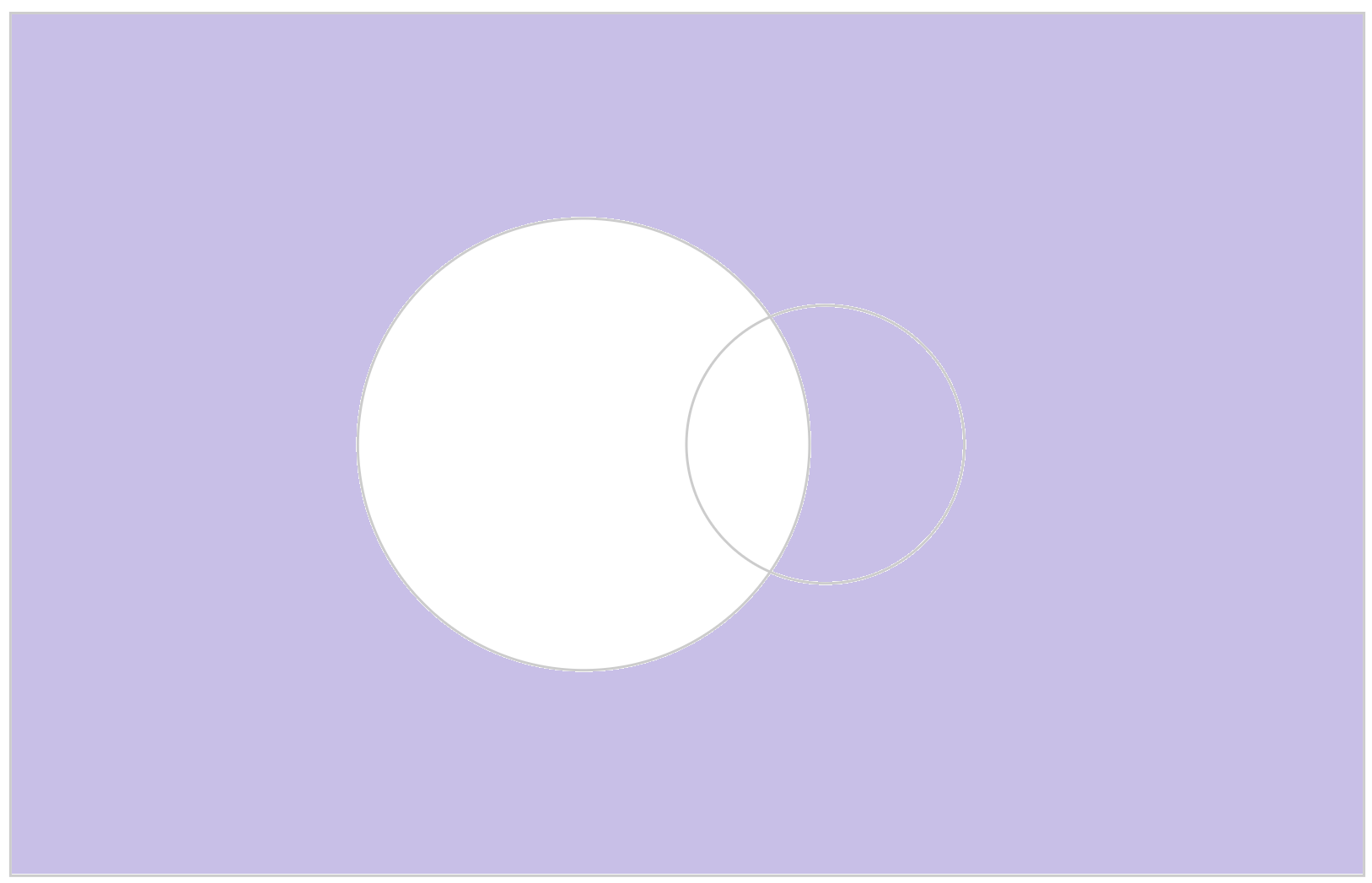
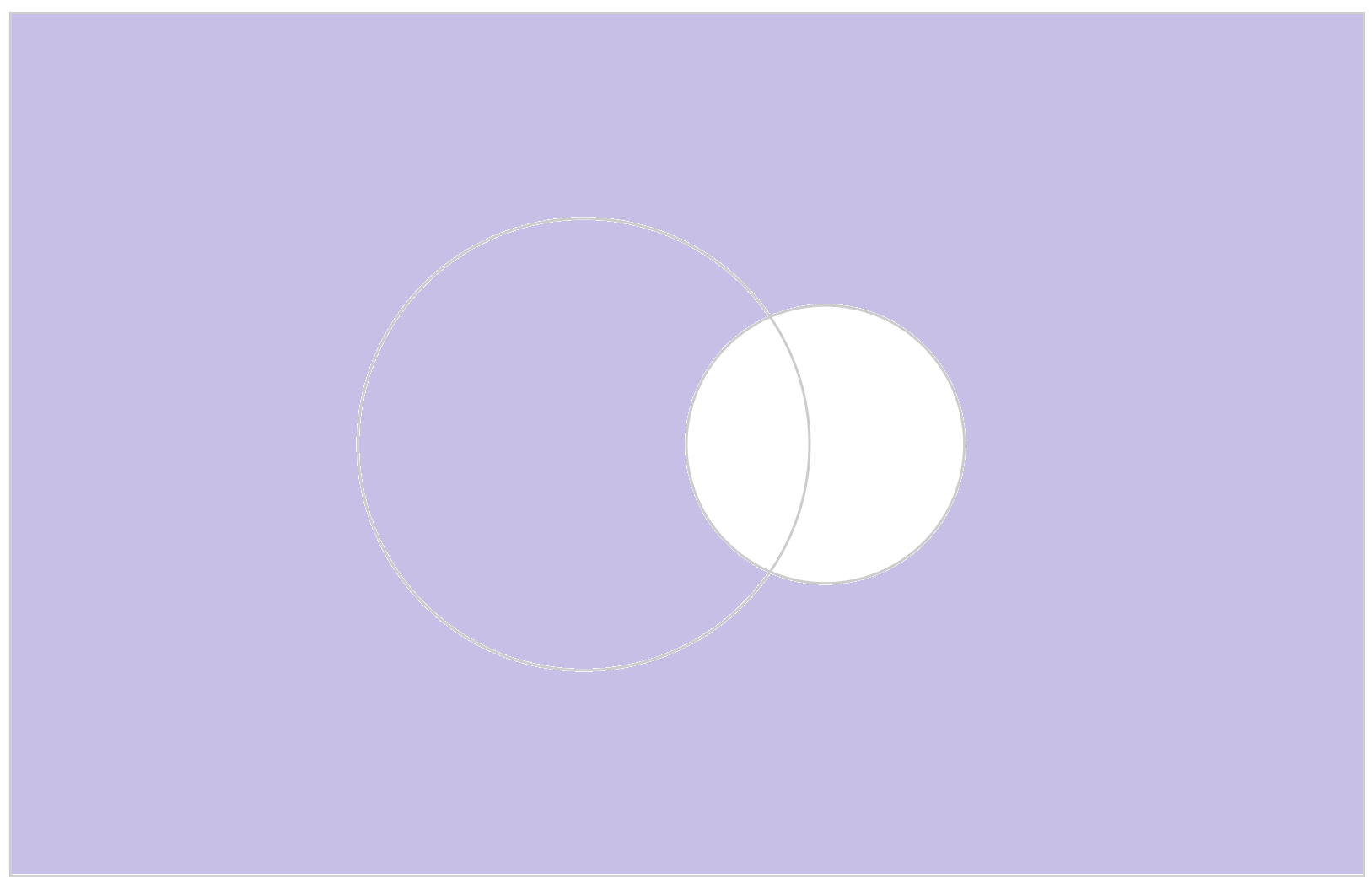
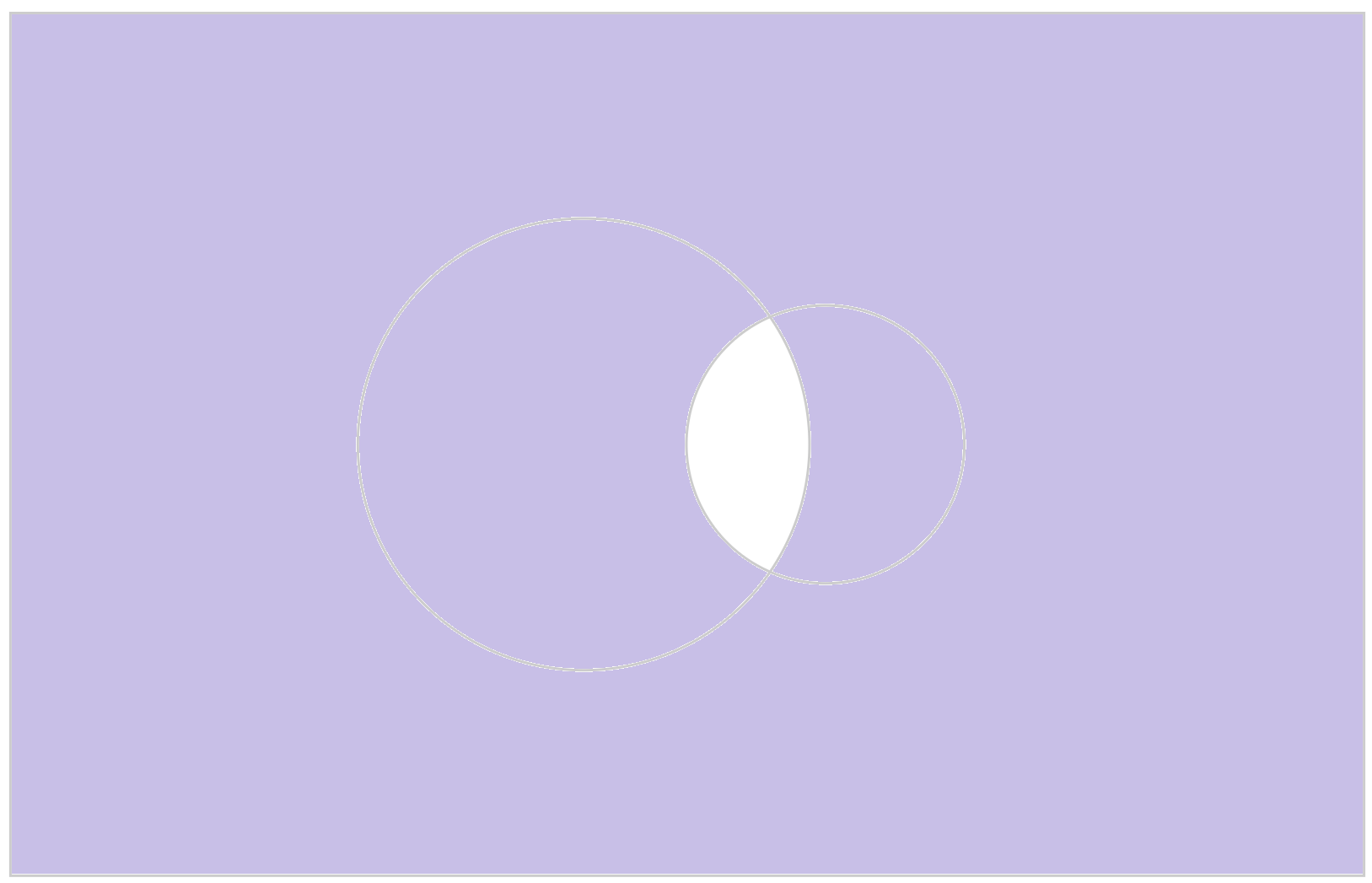
考慮集合與集合間的關係,我們便可以從已知的集合構作新的集合。我們可以透過溫氏圖(Venn diagram)直觀地表達,以顯示所有交疊的區域。
在指定空間\(\;S\;\)中給定一個集合\(\;A\),考慮所有不包含於\(\;A\;\)的元素,便可以得到它的餘集\(\;\overline{A}\),用符號表示就是:
\[\overline{A}=\{x\in S:x\notin A\}。\]




給定兩個集合\(\;A\)、\(B\),考慮所有同時存在於\(\;A\;\)和\(\;B\;\)的元素便可以得到它們的交集\(\;A\cap B\),用符號表示就是:
\[A\cap B=\{x:x\in A\;且\;x\in B\}。\]
我們也可以考慮所有存在於\(\;A\;\)或\(\;B\;\)的元素來構作它們的併集,用符號表示就是:
\[A\cup B=\{x:x\in A\;或\;x\in B\}。\]
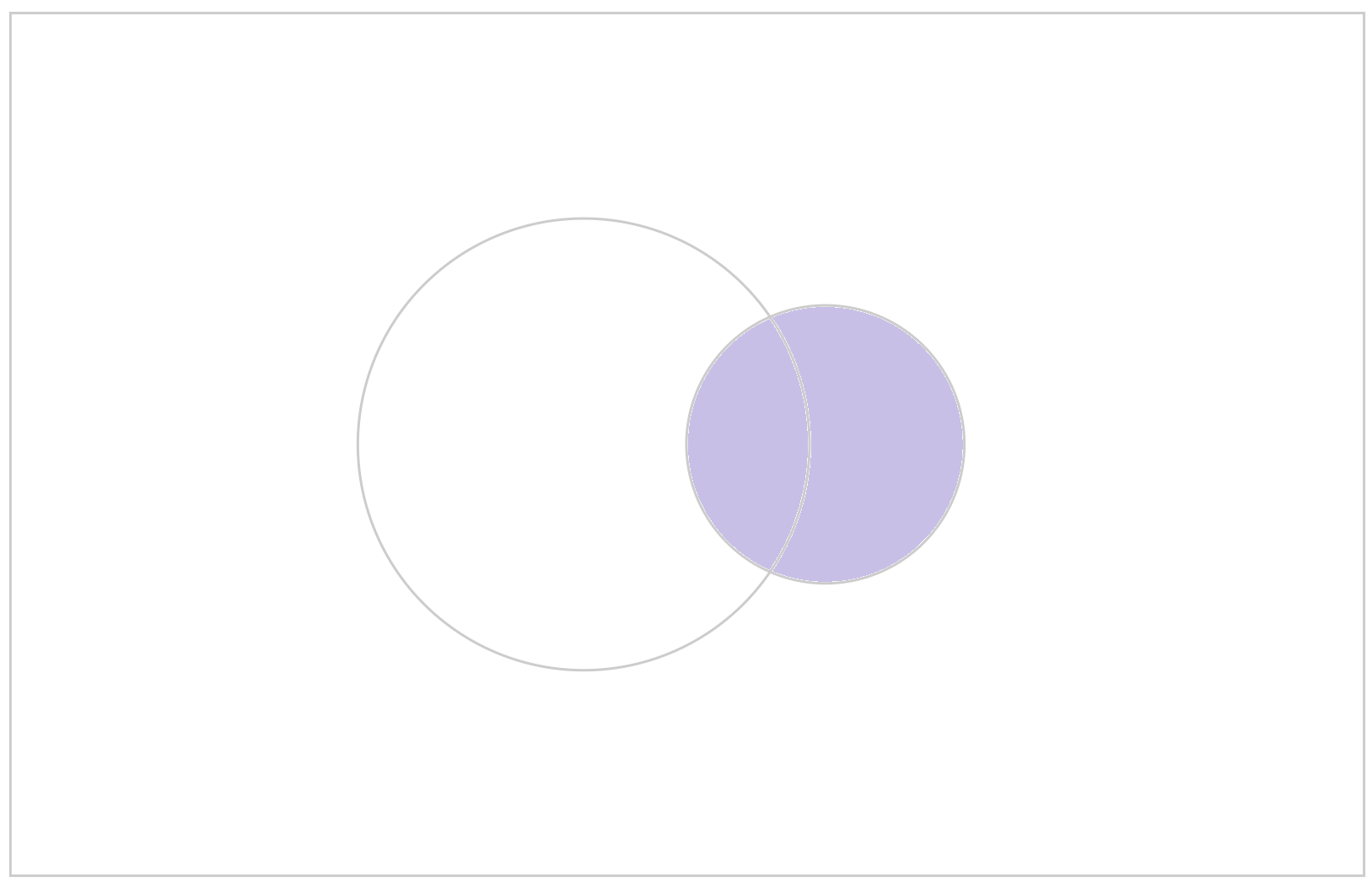
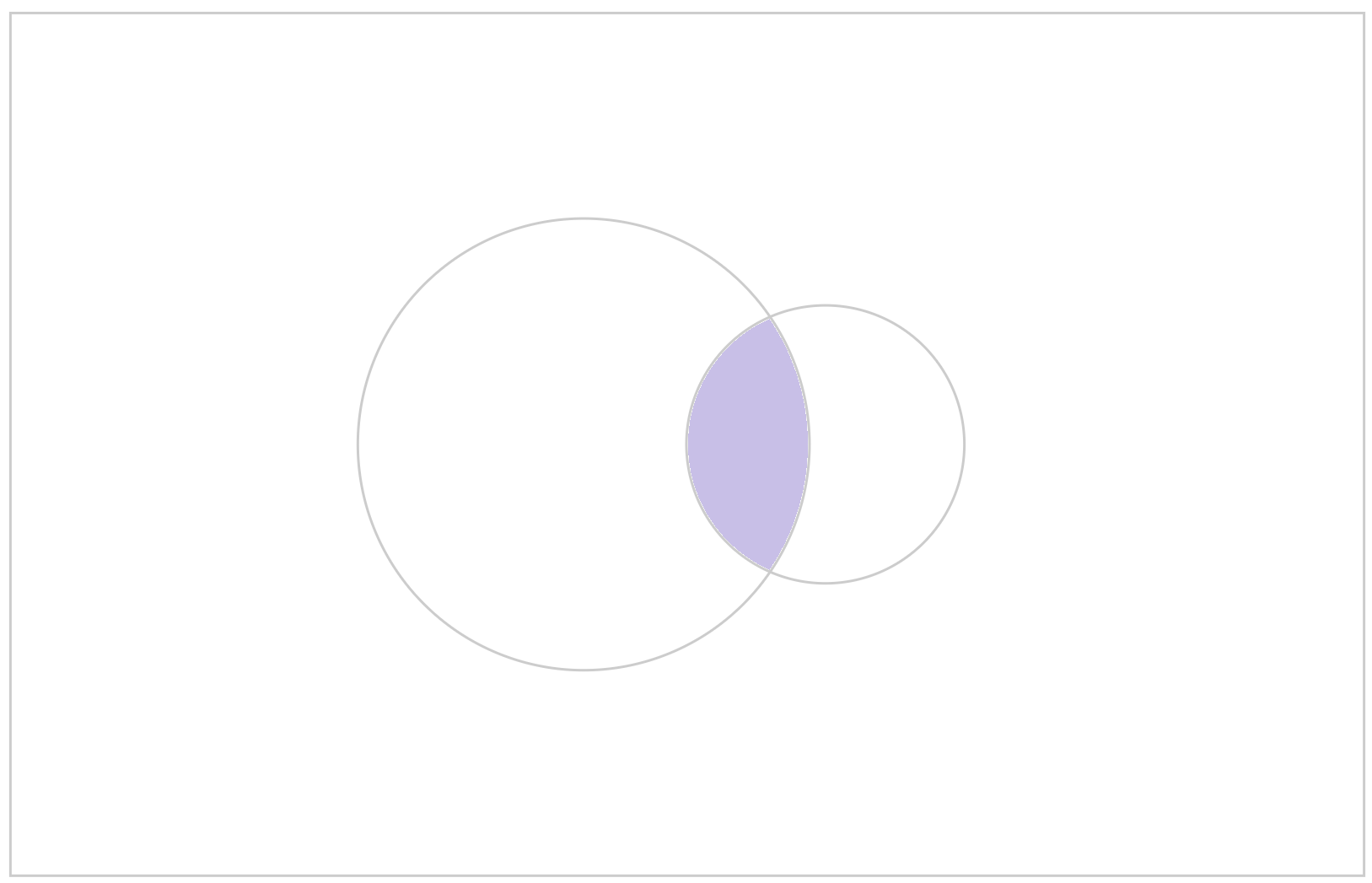

你可以從互動素材找到這些集合。
| 一些恆等式——你能從互動素材印證這些規律嗎? |
|---|
| \(\;\displaystyle{A=(A\cap B) \cup (A\cap \overline{B})}\;\) |
| \(\;\displaystyle{A=(A\cup B) \cap (A\cup \overline{B})}\;\) |
| \(\;\displaystyle{\overline{(X\cap Y)}=\overline{X}\cup \overline{Y}} \;\) |
| \(\;\displaystyle{|X|+|Y|=|X\cap Y|+|X\cup Y|}\;\) |