晶胞是晶體結構中最小的單位。當我們把晶胞重複排列,就可以築成整個結構。
情況就類似在聚合物中,只要將重複單位不斷重複排列,就可以獲得聚合物鏈的結構。

配位數就是指在一個晶格中包圍一個原子(或離子)的原子(或離子)的數目。
在考慮金屬原子的排列結構時,我們可從它的晶胞開始。其中一個考慮條件是這個晶胞內原子(或離子)數目。
如果一個原子完全陷於晶胞之中,則這個原子只屬於這個晶胞,即這個晶胞完全擁有該原子。
如果一個原子處於晶胞的平面上,則這個原子由\(\;2\;\)個晶胞共同擁有,即每個晶胞擁有\(\;1/2\;\)個原子。
如果一個原子處於晶胞的邊上,則這個原子由\(\;4\;\)個晶胞共同擁有,即每個晶胞擁有\(\;1/4\;\)個原子。
如果一個原子處於晶胞的角上,則這個原子由\(\;8\;\)個晶胞共同擁有,即每個晶胞擁有\(\;1/8\;\)個原子。
體心立方結構中,每個原子都被\(\;8\;\)個原子包圍:\(4\) 個上一層的原子及\(\;4\;\)個下一層的原子。
因此,在體心立方結構中,原子的配位數是\(\;8\)。
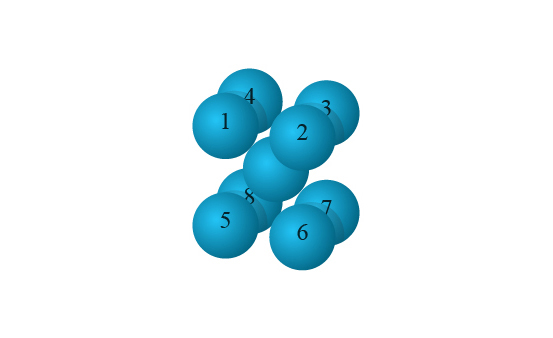
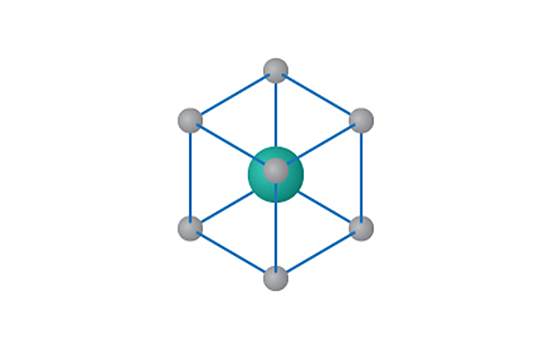
在這個晶胞中,共有\(\;1\;\)個完整的原子在晶胞內,並且有\(\;8\;\)個原子在晶胞的角上。
因此,\[晶胞所含的原子數目=\left[ 1+8\times \frac{1}{8} \right]\]
\[晶胞所含的原子數目=2\]

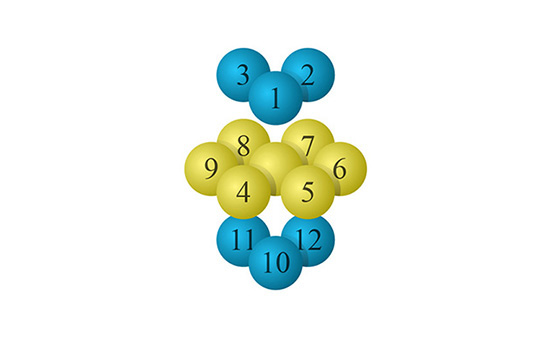
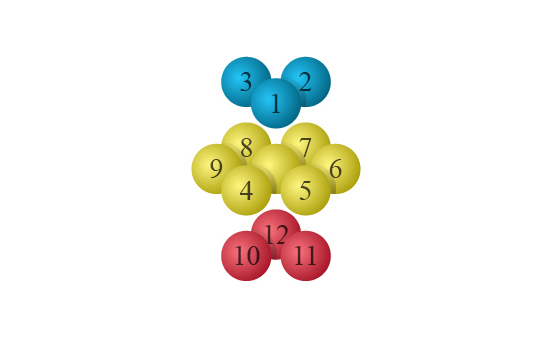
六方緊密結構中,每個原子都被\(\;12\;\)個原子包圍:\(6\;\)個同層的原子、\(3\;\)個上一層的原子及\(\;3\;\)個下一層的原子。
因此,在六方緊密結構中,原子的配位數是\(\;12\)。
很多金屬都是以六方緊密結構或立方緊密結構的方式來排列原子的,這使每個金屬原子都能和最多數目的相鄰原子接觸,生成金屬鍵。
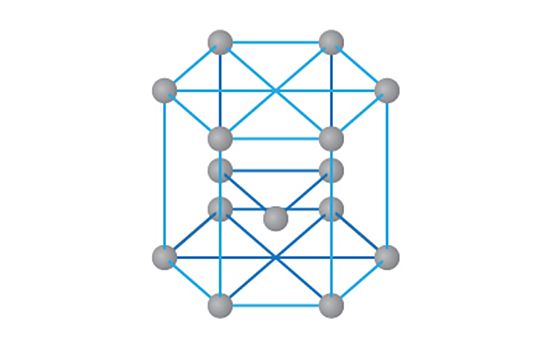
六方緊密結構的晶胞呈六角柱體。
在這個晶胞中,共有\(\;3\;\)個完整的原子在晶胞內;另外有\(\;2\;\)個原子在晶胞的邊上,並有\(\;12\;\)個原子在晶胞的角上。
因此,\[晶胞所含的原子數目=\left[ 3+2\times \frac{1}{2}+12\times \frac{1}{6} \right]\]
\[晶胞所含的原子數目=6\]

立方緊密結構中,每個原子都被\(\;12\;\)個原子包圍:\(6\;\)個同層的原子、\(3\;\)個上一層的原子及\(\;3\;\)個下一層的原子。
因此,在立方緊密結構中,原子的配位數是\(\;12\)。
很多金屬都是以六方緊密結構或立方緊密結構的方式來排列原子的,這使每個金屬原子都能和最多數目的相鄰原子接觸,生成金屬鍵。
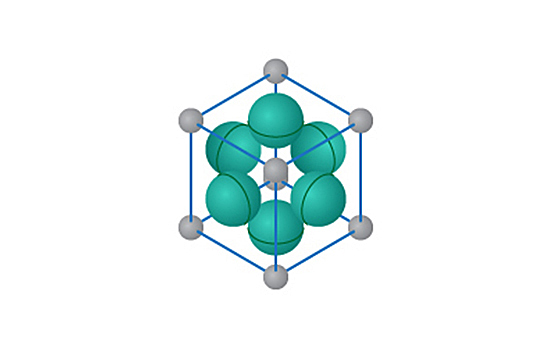
在這個晶胞中,共有\(\;6\;\)個原子在晶胞的邊上,並且有\(\;8\;\)個原子在晶胞的角上。
因此,\[晶胞所含的原子數目=\left[ 6\times \frac{1}{2}+8\times \frac{1}{8} \right]\]
\[晶胞所含的原子數目=4\]
